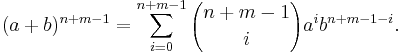Radical of an ideal
In commutative ring theory, a branch of mathematics, the radical of an ideal I is an ideal such that an element x is in the radical if some power of x is in I. A radical ideal (or semiprime ideal) is an ideal that is its own radical (this can be phrased as being a fixed point of an operation on ideals called 'radicalization'). The radical of a primary ideal is prime.
Radical ideals defined here are generalized to noncommutative rings in the Semiprime ring article.
Contents |
Definition
The radical of an ideal I in a commutative ring R, denoted by Rad(I) or √I, is defined as
Intuitively, one can think of the radical of I as obtained by taking all the possible roots of elements of I. Rad(I) turns out to be an ideal itself, containing I.
The easiest way to prove that the radical of I of a ring A is an ideal is to note that it is the pre-image of the ideal of nilpotent elements in 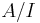 .[1] In fact, one often takes this identification as a definition of radical.
.[1] In fact, one often takes this identification as a definition of radical.
If an ideal I coincides with its own radical, then I is called a radical ideal.
Examples
Consider the ring Z of integers.
- The radical of the ideal 4Z of integer multiples of 4 is 2Z.
- The radical of 5Z is 5Z.
- The radical of 12Z is 6Z.
- In general, the radical of mZ is rZ, where r is the product of all prime factors of m that are less than m. (see radical of an integer)
The radical of a primary ideal is prime.
The nilradical of a ring
Consider the set of all nilpotent elements of R, which will be called the nilradical of R (and will be denoted by N(R)). One can easily see that the nilradical of R is just the radical of the zero ideal (0). This permits an alternative definition for the (general) radical of an ideal I in R. Define Rad(I) as the preimage of N(R/I), the nilradical of R/I, under the projection map R→R/I.
To see that the two definitions for the radical of I are equivalent, note first that if r is in the preimage of √(R/I), then for some n, r n is zero in R/I, and hence r n is in I. Second, if r n is in I for some n, then the image of r n in R/I is zero, and hence r n is in the preimage of √(R/I).
This alternative definition can be very useful, as we shall see right below. See #Properties below for another characterization of the nilradical.
Properties
- If P is a prime ideal, then R/P is an integral domain, so it cannot have zero divisors, and in particular it cannot have nonzero nilpotents. Hence, the nilradical of R/P is {0}, and its preimage, being P, is a radical ideal.
- By using localization, we can see that Rad(I) is the intersection of all the prime ideals of R that contain I: Every prime ideal is radical, so the intersection J of the prime ideals containing I contains Rad(I). If r is an element of R which is not in Rad(I), then we let S be the set {rn|n is a nonnegative integer}. S is multiplicatively closed, so we can form the localization S-1R. Form the quotient S-1R/S-1I. By Zorn's lemma we can choose a maximal ideal P in this ring. The preimage of P under the maps R→S-1R→S-1R/S-1I is a prime ideal which contains I and does not meet S; in particular, it does not meet r, so r is not in J.
- In particular, the nilradical is equal to the intersection of all prime ideals containing the 0 ideal, but all ideals must contain 0 so the nilradical can alternatively be defined as the intersection of the prime ideals.
Applications
The primary motivation in studying radicals is the celebrated Hilbert's Nullstellensatz in commutative algebra. An easily understood version of this theorem states that for an algebraically closed field k, and for any finitely generated polynomial ideal J in the n indeterminates 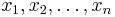 over the field k, one has
over the field k, one has
where
and
Another way of putting it: The composition 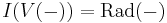 on the set of ideals of a ring is in fact a closure operator. From the definition of the radical, it is clear that taking the radical is an idempotent operation.
on the set of ideals of a ring is in fact a closure operator. From the definition of the radical, it is clear that taking the radical is an idempotent operation.
See also
References
- ^ A direct proof can be give as follows: Let a and b be in the radical of an ideal I. Then, for some positive integers m and n, an and bm are in I. We will show that a + b is in the radical of I. Use the binomial theorem to expand (a+b)n+m−1 (with commutativity assumed):
- i ≥ n
- n + m − 1 − i ≥ m.
- Eisenbud, David, Commutative Algebra with a View Toward Algebraic Geometry, Graduate Texts in Mathematics, 150, Springer-Verlag, 1995, ISBN 0-387-94268-8.
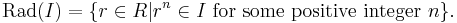

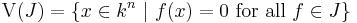
![I(S) = \{f \in k[x_1,x_2,\ldots x_n] \ |\ f(x)=0 \mbox{ for all } x\in S \}.](/2012-wikipedia_en_all_nopic_01_2012/I/ab36ec89341f75373f5fa8df36ade4b4.png)